第二节 变异与变量

一、变异（variation）
宇宙间没有任何完全相同的个体，它们总是或多或少的存在着差异，即在不同的条件下，不同个体的同种指标在相同的条件下，对内外环境影响的反应可以出现互不一致的结果。例如，性别有男女之分，年龄有大小之分，即使同性别同年龄的一批儿童，在相同条件下生长，他们的身高、体重及肺活量等也可能完全不同，有的体重重一些，有的轻一些。统计学上把这种个体间的差异称为“变异”。为了进一步说明这个问题，特举下例。
现有3组7周岁男性儿童，他们的体重测量（kg）结果如下：

甲组：12131315161617
乙组：13141415151516
丙组：11141612181417
经过计算，这3个组的均数都是1457kg。顾名思义，均数只反映平均水平，而3组中的个体是相同性别、相同年龄的体重，各组7个数据间参差不齐的程度（即变异）是不一样的，或者说三组数据的离散程度不同。
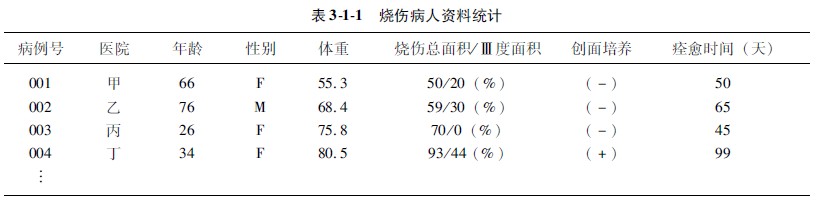
由于正常个体存在变异，在患病与治疗过程中这种变异也必然存在。如用某药治疗深Ⅱ度烧伤创面共50个，瘢痕发生率为30%，但在同样条件下再治疗50个，瘢痕发生率就不一定为30%，可能大于30%，也可能小于30%。产生这种现象的主要原因是受变异因素的影响，故必须用统计学方法处理才能把握事物的本来规律，解决两次试验结果差异的内在联系，使科研结论建立在更科学的基础上。上例结果除了说明个体的体重经常出现变异之外，同时也告诉我们，在计算小儿烧伤休克补液量时，对体重的估计要力争做到准确，仅用小儿体重=2×年龄+（7～8kg），即2倍年龄＋7或＋8这个程式的计算值误差较大。通过计算可以看出，甲组的极差为5（17-12=5），乙组的极差为3（16-13=3），丙组的极差为7（18-11=7），即第3组的体重离散程度较大。
由此可见，只有把平均数与变异指标结合起来，才能说明一组资料的特征。这些变异属于偶然性质的，故将这种由一些偶然因素引起的个体间的差异称为变异。变异既是事物间的反映，也是统计的前提，没有变异也就无须统计了。统计学较常用的变异指标有：极差、四分位数间距、均差、方差、标准差、变异系数等。上例的正确表示方法应是均数±标准差。
二、变量（variable）
在统计工作中，应根据研究目的，对某个或某些被研究的个体特征（也称研究指标或项目）实施观测，这些特征（指标或项目）即为变量。变量的观察值（即变量值）构成数据或资料。或者说当对每个观察单位的某项特征进行观察和测量时，被观察的这项特征即称为变量，观察测量的结果称为变量值。变量值可以是定性的，也可以是定量的（表311）。