第二节 计数资料的显著性检验

对于计数资料这些相对数我们只知它们的高低，不知其有无统计学意义，只有通过相对数的显著性检验方能明确。常用方法为U检验与χ2检验。
一、率的u检验
率的u检验是应用范围较为广的一种显著性检验方法，但是在用于样本率与总体率比较时，或两个样本率比较时，应当考虑其差异是否由于抽样误差所造成的。大样本的样本率分布近似正态分布，可用正态分布的规律检验样本率与总体率或两个样本率差异的显著性。其判断标准为：

（一）样本率与总体率的比较
样本率与总体率比较的目的是推断该样本所代表的总体率与已知总体率是否相同。公式为：

p为样本率，π为总体率，σP为率的标准误，由总体计算得出
示例343根据临床经验，胃十二指肠溃疡患者中，一般情况下有20%的病人会发生胃出血症状，现某医院观察烧伤病人152例，其中48例伤前有过胃出血病史，问伤前患有胃十二指肠溃疡的烧伤病人是否容易发生胃出血？
【解题步骤】
可将该例中胃十二指肠溃疡患者有20%发生胃出血率视为总体率π（是把人们公认或经验数值作为总体率）。
1建立检验假设：假设患有胃十二指肠溃疡病的烧伤病人胃出血率（p）与一般胃十二指肠溃疡患者的出血率（π）无差别，即样本率（P）是由总体率（π）中随机抽取的，两者无差别。事实上，实验研究结果总是有两种情况：一种是接受所建立的检验假设，一种是拒绝建立的检验假设。
①设前者为H0：π=π0；②设后者为H1：π≠π0。
2确立显著性水准：α=005
3计算u值：将示例343中数据代入公式（346）：

4确定P值：因为u=358，而358＞258，故P＜001。
5推断结论：在α=005水准上，拒绝H0，接受H1，因P＜001，所以有非常显著性差异，伤前患有胃十二指肠溃疡的烧伤病人，其胃出血率与一般胃十二指肠溃疡患者的出血率有本质差异，可认为患胃十二指肠溃疡的烧伤病人较一般胃溃疡患者容易发生胃出血。
（二）两个样本率比较的U检验
两个样本率比较的目的是推断两个样本各自代表的两个总体率是否相同。常用U检验和χ2检验：
U检验计算公式：

示例344如某医院对1 329例烧伤病人进行应激性溃疡出血的预防性治疗，有56例发生了胃出血，发病率为421%，1 670例伤情相似的病人未进行预防性治疗，其出血率达832%，问两组样本应激性溃疡出血的发病率有无差异？
【解题步骤】
1建立检验假设：H0：π1=π2，H1：π1≠π2。
2确定显著性水平：α=005。
3计算u值：n1=1329，X1=56，P1=00421（56/1329），n2=1670，X2=139，P2=00823（139/1670）。
代入公式（349）、（3410）、（347）：

4确定P值：因425＞258，故P＜001。
5推断结论：在α=005的水准上，拒绝H0，接受H1。因P＜001，差异有高度显著性，故认为预防性治疗组与对照组的应激性溃疡出血率有本质不同，预防组应激性溃疡出血发生率低于对照组，预防治疗有效。
二、χ2检验
χ2检验是英国统计学家Kpearson提出的，后经Yates校正改进，现已成为专用于两组百分率的常用显著性检验公式。“χ”为希腊字母，读音为“Kai”，故χ2检验法又称“卡方法”。应用范围与U检验不完全相同，前者主要针对样本率与总体率进行比较，也可用于两个样本率的比较；而χ2检验主要用于推断两个及两个以上总体率（或构成比）之间的检验，检查两个分类变量之间有无关系（或关联）。
（一）χ2检验基本公式与计算方法
χ2检验的基本公式：

A为实际观察数，T为理论计算值， ∑（希腊字母，读音Sigma）表示总和。举例解释其方法及原理。
示例345某医院对过去治疗的烧伤并发败血症的病例进行回顾性总结，205例大面积烧伤病人并发败血症的例数为43，而134例中等烧伤面积病人并发败血症的例数为13，问败血症的发生与烧伤面积有无关系？
【解题步骤】
1将调查资料列入表（表342）中：

2建立“检验假设”（无效假设），即假如大面积与中等面积烧伤组的败血症发生率之间没有本质差别，说明败血症的发生率（21%和97%）来自同一总体，这种差别是由抽样误差造成的。根据这个假设，可以用两个组的合计发病率（165%）为假设的理论总体，并以此作为计算值的理论基础。
3计算各组的理论数T值：理论数值是根据检验假设推论的两组病人数中应有的发生败血症人数，即两组都按165%患病率计算，应当有多少人患病与不患病。大面积烧伤组205人，乘以合计患病率165%，便是大面积烧伤组理论上应当发生败血症的人数（205×165%=3383），即为理论值；而未发生败血症的人数为（205-3383=17117）17117。同理，再求出中等烧伤面积组病人的理论值为2211，不发生败血症的理论值为（134-2211=11189）11189。
将计算的理论值汇入表343中。

4代入χ2值公式（3411）计算χ2值：

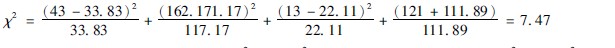
χ2值无单位，与它相应的概率为5%的χ2值（χ2 005）和概率为1%的χ2值（χ2001），可由卡方简明界值表344中查出。
如果上述检验正确，A-T差值不会太小，如A-T相差太大，检验假设成立的可能性就不大。
5根据χ2值与自由度查χ2值表：首先确定自由度（df或n′或r，），因四格表中有四个理论值，只要先用乘除法求出任何一个，其余三个可用减法求出。这种必须先用乘除法求出理论值的格子数叫自由度。计算方法：
n′=（行数-1）（列数-1），四格表中为两行、两列，故：
n′=（2-1）（2-1）=1。
查简明χ2值表（表344，或查有关书籍卡方界值表）：当n′=1时，χ2005=663，本例χ2=747，大于663，已超过χ2005=663水平，但小于χ20005=788水平，故P＜001。

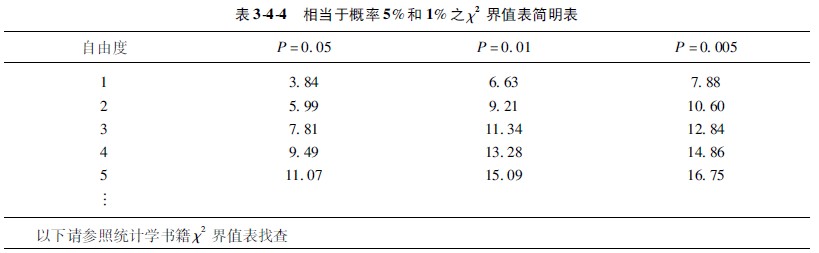
（二）四格表资料的χ2检验（两个样本率的比较）
四格表资料的χ2检验法是应用最为广泛和最为方便的一种方法，它所检验的仅是两个率的比较。基本模式图、公式和结果判断标准如下：

4计算步骤：
（1）先将题目中的数据按四格表模式图形式制表排列（用实际数字，不用百分率）。
（2）代入公式(3412)，计算χ2值，χ2值是统计值，数值越大统计意义越大。
（3）根据χ2值的大小，按P值判断标准确定P值大小。
（4）做出统计结论。
示例346用甲法治疗大面积烧伤（甲组）71例，有52例并发全身性感染，用乙法治疗的大面积烧伤（乙组）42例，有3例并发全身性感染。问两组感染发生率有无统计学差异？
【解题步骤】
1按四格表模式重新制表（表347）：

2计算χ2值(公式342)：

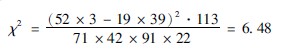
3计算自由度：因为自由度（n′）=1{（行-1）（列-1）=（2-1）（2-1）}，故本研究自由度为1（1×1）。
4按表344标准确定P值：因χ2值在384和663之间，故P＜005，组间有显著性差异。
5结果判断：因P＜005，说明乙法治疗的大面积烧伤病人并发全身性感染的机会低于甲组。
（三）行×列表资料的χ2检验
以上讲的是两个样本率的检验，用四格表法，但当行数或列数大于2时，应当用行×列表资料的χ2检验，又称R×C表资料。基本公式：

A为各格子的实际频数，nR、nC为各实际频数所对应的行的合计数和列的合计数，N为总合计数。
该公式是由基本公式转换而来，不需要求理论频数，方便实用。
示例337甲乙丙三所医院同期对某药进行抗感染疗效观察，甲院观察了29例，有效（23例）率为793%，乙院观察了44例，有效(14例)率为318%，丙医院观察了11例，有效（3例）率为273%（资料见表348）。问3所医院抗感染治疗的总体有效率是否有显著意义？

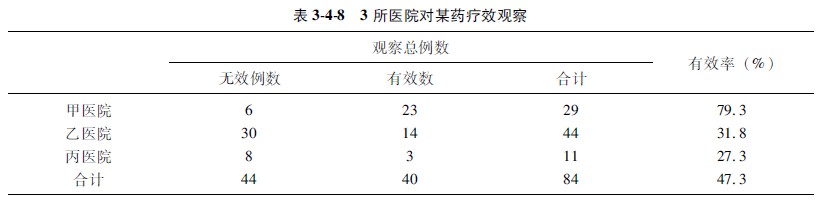
【解题步骤】
1建立检验假设：H0：3所医院的有效率相等，π1=π2；H1：3所医院的有效率不相等，H1：π1≠π2。
2确定显著性水平：α＝005。
3根据χ2基本计算公式（3413）计算χ2值：

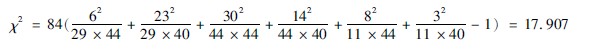
4确定自由度（n′）=（2-1）（3-1）= 2。
5查χ2值表确定P值：查表344可知，χ2005（2）=1060，今χ2=17907，＞χ20005(2)，故P＜0005。
6推断结论：在α=005水准上，拒绝H0，接收H1，故该药在三所医院的抗感染效果存在统计学差异（P＜0005）。
（四） 二列多格资料χ2值检验
二列多格资料χ2值检验也称多个样本率的比较，其目的是推断它们所代表的总体率是否相等。该类资料的基本数据有R行（样本个数），2列（指样本的阳性数与阴性数），所以又叫R×2列联表或列联表(contingency table)。
公式同基本公式（3413），计算出的资料可以进行相关分析。
示例348（百分比相互比较）：某医院观察严重烧伤病人早期延迟治疗对休克发生率有无影响，观察时间分别为伤后大于18小时（甲组）、伤后6～18小时（乙组）和6小时以内（丙组）3个接受治疗小组，结果汇于表349中。问延迟治疗对烧伤休克的发生率有无统计学差异，或相互之间有无关联？

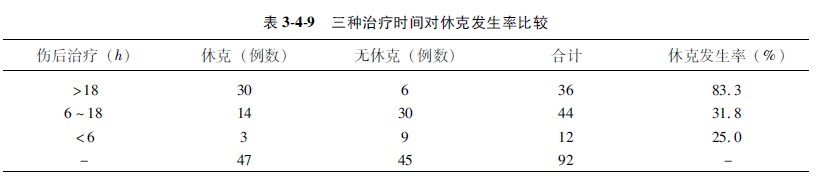
【解题步骤】
1建立检验假设：设H0：三种不同治疗时间休克发生率相等；设H0：π1=π2；三种不同治疗时间休克发生率不完全相等，H1：π1≠π2。
2确定显著性水平：α=005。
3计算χ2值：将表349中的数字代入公式3413，得：

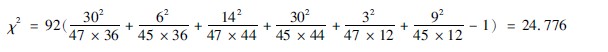
4计算自由度：（n′）=（2-1）（3-1）= 2。
5确定P值：因n′=2，查χ2值表（344），χ20005（2）=1060，本研究χ2＝24776＞χ20005（2）（1060）水平，P＜0005。
6推断结果：在α=005水准上，拒绝H0，接受H1，因P＜0005，差异有高度显著性，故认为严重烧伤病人早期接受治疗对休克发生率有明显影响作用，即可降低休克发生率。
7为了进一步说明它们之间的密切关联程度，可根据公式计算关联系数：

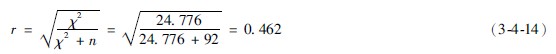
根据四格表的pearson列联系数值r在0～1之间。r值愈接近0，说明两个分类变量的关系愈弱，r值愈接近1，说明关系愈密切。因为r=0462，说明延迟治疗时间与休克发生率具有一定的关联性。
示例349（样本结构比相互比较）：某院2004年收治小儿烧伤145例，致伤因素：热液150例，火焰10例，电流7例，其他23例；成人烧伤188人，致伤因素：热液50例，火焰48例，电流18例，其他72例（资料见表3410），问小儿烧伤原因与成人烧伤原因相互之间是否有关联性？

【解题步骤】
1建立检验假设和确定显著性水平：①设H0：两组病人伤因构成相等，H0：π1=π2；②设H1：两组病人伤因构成不完全相等，H1：π1≠π2。
2显著水平：α=005。
3计算χ2值：可将表3410中的数字代入公式（3413），得：

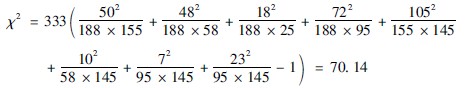
4计算自由度：（n′）=（2-1）（4-1）= 3。
5确定P值：n′=3，查χ2值表（344），χ20005（3）=1284，今χ2=7014，故P＜0005。
6推断结果：在α=005水准上，拒绝H0，接受H1，因P＜0005，差异有非常显著意义，故认为小儿烧伤病人的致伤因素构成比与成人不同，说明小儿以热液烫伤多见，其他伤因构成比低于成人组。
7为了进一步说明它们之间的密切关联程度，可根据公式3414计算关联系数：

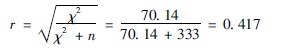
因为r=0417，说明儿童烧伤伤因与成年人烧伤伤因之间具有一定的关联性。由于儿童热液烫伤发生率为724%，成人热液烫伤发生率为266%，两者是否存在显著性差异，需要进行两两比较方可明确。
（五） 多列多格资料χ2值检验
临床经常遇到3组或3组以上的多格资料，其计算方法仍以公式（3413）为基础 。现举例说明：
示例3410（计数资料相关分析）：某烧伤中心观察了176例吸入性损伤病人的不同伤情与呼吸困难的各自例数，问呼吸困难程度与吸入损伤伤情之间有无关联性（数据资料汇于表3411中）？

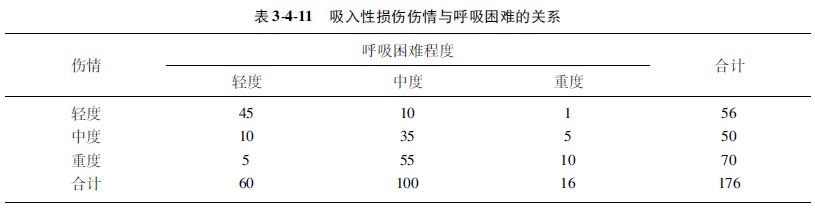
【解题步骤】
本例的设计和分析目的与上述例子不同。它并非是两个样本率与总体率、多个样本率与总体率或构成比之间的比较，而是单一样本自身的比较，每个对象分别按两种标志分级（伤情与呼吸困难），属于双相率的计算，目的是推测两种标志之间有无相关性。
1建立检验假设：①设H0：呼吸困难程度与吸入性损伤程度无关；②设H1：呼吸困难程度与吸入性损伤程度有关。
2确定显著水准：α=005。
3计算χ2值：将表3411中的数字代入公式3413，得：

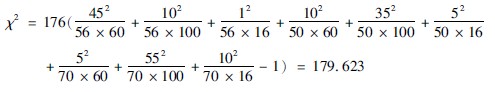
4计算自由度：（n′）=（3-1）（3-1）= 4。
5确定P值：n′=4，查χ2界值表（324），χ20005(4)=1486，本研究χ2=179623，＞χ20005(4)（1486）水准，P＜0005。
6推断结果：在α=005水准上，拒绝H0，接受H1，因P＜0005，差异有高度显著性，故认为呼吸困难程度与吸入性损伤程度关联密切。
7为了进一步说明它们之间的密切关联程度，可根据公式（3414）计算关联系数：

因为r=07316，说明呼吸困难程度与吸入损程度具有明显的关联性，即吸入损伤越重，呼吸困难越严重。
（六） 配对计数资料的χ2检验

计数资料的配对设计常用于两种检验方法，如培养方法、诊断方法的比较。其特点是对样本中的各观察单位分别用两种方法处理，然后观察两种方法的结果。此类资料可用配对χ2检验，比较两个率之间是否有差异。从配对设计来说，配对计数资料与前边所介绍的配对计数资料是相同的，都是把两种处理因素分别施加于条件相似的受试对象上，或先后施于同一对象上。配对记录试验结果如为计量资料，即属计量配对资料；若结果为计数资料，即属于计数配对资料。配对计数资料的χ2检验包括两个内容：①分析它们的相关关系；②分析处理结果有无差异。
示例3411：100个深Ⅱ度烧伤创面，每个创面分别用两种方法（甲法与乙法）诊断。结果：甲法阳性者为67个，乙法阳性者50个；其中甲乙两法均阳性者（a）39个，甲乙两法均阴性者（d）22个，甲法阳性乙法阴性者（d）28个，乙法阳性甲法阴性者（c）11个（资料见表3412）。问甲乙两种方法的诊断结果有无关联及统计学差异？
【解题步骤】
第一步：分析两种诊断结果有无相关关系，每个对象按两种处理结构分组，故可用四格χ2检验公式计算，推断两种诊断方法之间有无相关关系：
1建立检验假设：①设H0：甲乙诊断方法之间无关；②设H1：甲乙诊断方法之间有关。
2确定显著水准：α=005。

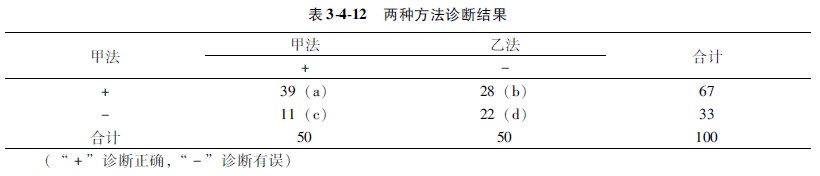
3计算χ2值：将表3412中的数字代入公式3412，得：

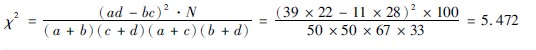
4计算自由度：（n′）=（2-1）（2-1）=1。
5确定P值：n′=1，查χ2值表（344），χ2005=3841，χ2001=6635，本研究6推断结果：在α=005水准上，拒绝H0，接受H1，因P＜005，差异有显著性，故认为两种诊断程度关联密切。
第二步：计算两种处理结果有无差别：计算公式为（3415）：

1建立检验假设：①设H0：两总体b=c；②H1：两总体b≠c。
2确定显著水准：α=005
3计算χ2值：将表3412中的数字代入公式3415，得：

4自由度：n′=1。
5确定P值：n′=1，查χ2值表（344），χ2005=3841，χ2001=6635，本研究χ2=6564，介于χ20005和χ2001水准之间，故P＜005。
6推断结果：在α=005水准上，拒绝H0，接受H1，因P＜005，差异有显著性，故认为甲乙两种诊断方法的确诊率不同，甲法的确诊率高于乙法。
7关联性分析：根据公式3414计算关联系数：

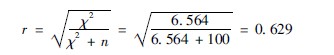
因为r=0629，说明甲乙两种方法的诊断结果关联性较强，甲法优于乙法。
（七）两个小样本的χ2检验方法
因为χ2检验是以一条光滑曲线为基础，大样本所得的概率与其真正概率很接近。当为小样本时，如n＜40（有人认为n＜50）时，用前边讲的大样本比较的u检验或χ2检验公式计算结果都不准确，或偏倚较大，需要采用小样本校正公式计算。两个小样本的检验方法有两种：一种是样本（n）偏小；一种是四格表中有理论频数中出现0或1时。现举例说明：

1小样本校正公式（3416）：

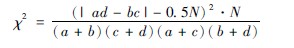
示例3312：用甲乙两种药物治疗糖尿病坏疽创面各30个，甲药组瘢痕发生率为70%，乙药组癜痕发生率为50%。问两组之间的疗效有无统计学差异？
【解题步骤】
（1）根据题中数据列表3413：

（2）将表3413中数字代入公式(3416)，得：

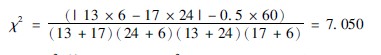
（3）结果判断：因n′=1，χ2值=7050＜χ2001（6635），故P＜001。组间有非常显著差异。
（4）结论：甲药治疗的创面瘢痕发生率低于乙药治疗组。
小样本率的χ2公式计算结果优于大样本率的χ2公式，尤其在其他检验公式所得概率接近检验水准时，宜用小样本率的χ2公式。目前许多统计学者认为：①小样本率的χ2公式误差最小，最为常用；②过去有一种误解，只有当例数小于30时，或理论频数小于5时，χ2原公式计算值中有误差，否则不必进行校正。实践证明，只要是判断P=005或P=001的显著检验，用校正公式肯定优于基本公式，即使例数大于30，或理论频数大于5，采用校正公式也比χ2原计算方法误差小。
2 两组数据中有1或0的小样本资料计算：前边已叙述了小样本率的χ2计算公式与方法，但在实际工作中，小样本资料经常出现理论频数小于1的情况，即T＜1。这种资料不宜用小样本计算公式计算，更不能用四格表公式计算，但宜用四格表确切概率法计算。确切概率法是由RAFisher提出的，故又称Fisher确切概率检验。此法本不属于χ2检验范畴，但可作为四格表资料假设检验的补充。介绍如下：
确切概率法各种组合概率的计算公式（3417）为：

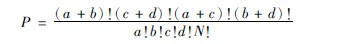
式中a、b、c、d的意义同表345，！为阶乘符号，N！=1×2×3×4×…×N，数学上规定！=1。一般计算器不能计算N≥70的阶乘，这种情况下用对数计算。
四格表中|A-T|值的特点：①各格相等，如表3414的A-T，a、d两格均为-14，b、c两格均为+14，其绝对值相等。因而计算某一四格表的|A-T|值时，只需计算表中任一格的|A-T|值即可；②依次增减四格表中任何一格的数据，可列出周边合计不变条件下各种组合的四格表，如示例3413中的五个四格表，分别计算其|A-T|值，列于表下。由此可见，两侧的|A-T|值较大，而中间的较小。
各种组合下累计概率的计算：①双侧检验：按公式3417分别计算两侧所有|A-T|值的各四格表的P值，然后相加，即为双侧检验的P值；②单侧检验：按研究目的，只计算一侧的所有|A-T|值等于及大于样本|A-T|值得四格表的P值，然后相加，即为单侧检验的P值。
示例3313：某医生用新旧两种方法治疗烧伤后贫血病人共计27例，结果汇于表3414中，问新旧药物的疗效有无差异？

【解题步骤】
（1）建立检验假设：H0：新药与旧药治愈率相等，即π1=π2；H1：新药与旧药治愈率不相等，即π1≠π2。
（2）确定显著水准：α=005。
（3）计算概率P：本组N=25＜40，且又T＜5，故宜用确切概率法。由表3414可见，最小周边合计数为4，故所有可能的组合有5种，分别为：

（4）确定P值，做出推断结论：P值应等于所有小于样本点的各种概率之和，本例符合样本点要求者为（1）、（2）、（5），因此，P值的组合为上述三点之和，即P=00166+01423+01079=02668。按α=005水准，P＞005。不能认为两种疗法的治愈率有统计学差异。
3查四格表显著性检验用表（C值表）法：此方法简便易行，本文不再叙述，可参照有关资料查询。