第六节 方差不齐时两小样本的均数检验

所谓方差不齐，是指两组的标准差相差太大，若相差超过一倍，可以肯定为方差不齐，较精确的计算方法是F值计算法，如按本方法计算，应明确被检验两组样本是否属于方差不齐，即首先应进行齐性检验确定其性质，然后进行t检验。
一、 两个方差的齐性检验
前面已经讲过，当两个样本均数进行比较时，要求相应的两组总体方差相等，即方差齐。但是，即使两组总体方差相等，两组样本方差也会由于抽样误差的影响而不相等。检验两组样本方差不等是否由于抽样误差所致，可用方差齐性检验，也就是检验σ21与σ22是否相等。方法用F检验，统计量F值按公式计算：

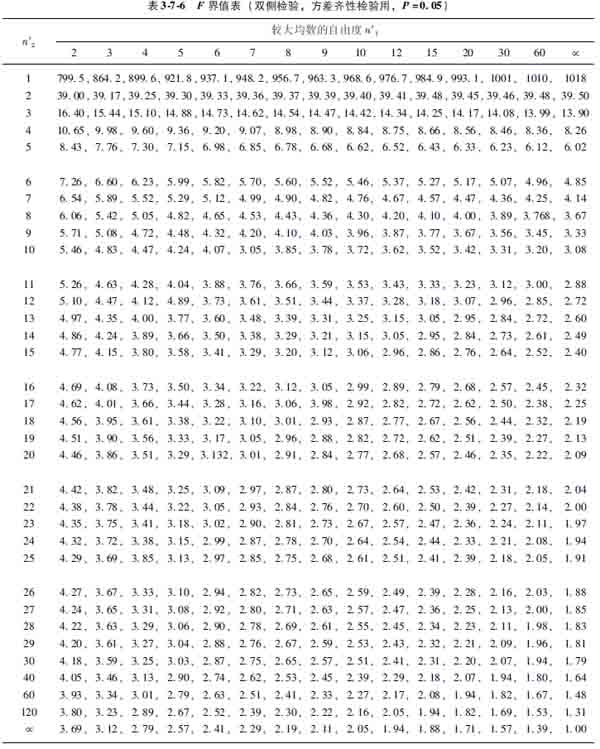
式中s21为较大样本的方差，s22为较小样的方差，相应的自由度分别为n′1和n′2，相应的样本含量分别为n1和n2。由于恒取s21>s22，故F值必然大于1，求得F值后查F界值表(方差齐性检验用表，表376），得P值(F值愈大，P值愈小)，作出结论。
示例377测得10名健康人和50例烧伤病人早期的RBC均值（1）和标准差（S），检验两组数据方差是否为齐性。
【解题步骤】
1建立检验假设，确定显著水准：①健康人：n=10， x1=621×109/L，s1＝179×109/L；②烧伤病人：n=50，x1=434×109/L，s2＝056×109/L。
H0：两总体方差相等，即σ21＝σ22； H1：两总体方差不等，即σ21≠σ22；α＝005
2计算检验统计量：按公式3710计算，得：

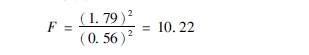
3确定P值，做出推断结论：以n′1=10-1=9，n′2=50-1=49，查F界值表（表376）。因1022＞233（n′2=60），P＜005，按α=005水准拒绝H0，接受H1，故可认为两总体方差不齐。
二、t′检验
若两个总体的方差不齐时，即σ21≠σ22时，两小样本均数的比较，可选择以下方法：①采用适当的变量变换，使之达到方差齐的要求；②采用不要求方差齐的方法比较其分布，如秩和检验；③采用近似法t′检验，由于t′不服从t分布，故需要按公式(3710)求界值t(系近似值)。公式分别为：

当确定检验水准α后，公式3712中的tα·n′1和tαn′2即可按n′1和n′2由表375查得，s2x1、s2x2分别为两均数的标准误的平方和。
仍以示例376为例：由于已知两者方差不齐，试比较两者均数有无差异。
H0：μ1=μ2；H1：μ1≠μ2；α＝005。

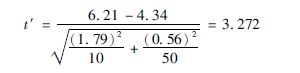
n′1=10-1=9，n′2=50-1=49。查t界值表（表371），得t0059=2262，t00549=2009。

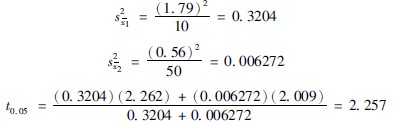
今t′>t′005，则P<005，按α＝005水准拒绝H0，接受Hl，故可认为两组的均数不等，烧伤病人RBC的均数大于健康者。